import numpy as np
import matplotlib.pyplot as plt
from scipy.sparse import diags
def build_W(n, t):
main_diag = [t] + [1 + t] * (n - 2) + [1 + t]
off_diag = [np.sqrt(t)] * (n - 1)
return diags([main_diag, off_diag, off_diag], [0, 1, -1], shape=(n, n)).toarray()
def conjugate_gradient(W, b, max_iter=None):
n = len(b)
x = np.zeros(n)
r = b - W @ x
p = r.copy()
rsold = r.dot(r)
residuals = [rsold]
if max_iter is None:
max_iter = n
for _ in range(max_iter):
Ap = W @ p
alpha = rsold / p.dot(Ap)
x += alpha * p
r -= alpha * Ap
rsnew = r.dot(r)
residuals.append(rsnew)
if rsnew < 1e-15:
break
p = r + (rsnew / rsold) * p
rsold = rsnew
return x, residuals
# Parameters
t = 0.1
n = 10
# Building problem and solution
W = build_W(n, t)
b = np.zeros(n)
b[0] = 1
x, residuals = conjugate_gradient(W, b)
# Graph
plt.figure(figsize=(10, 6))
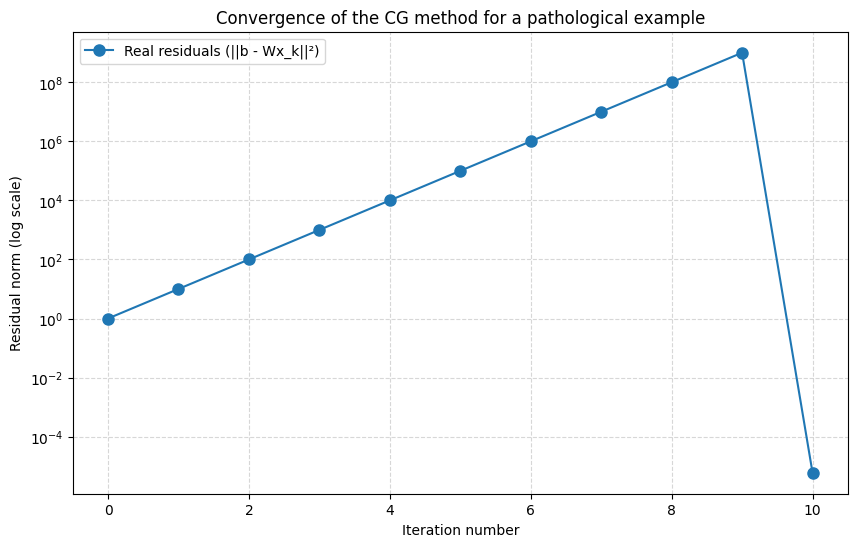
plt.semilogy(residuals, 'o-', label='Real residuals (||b - Wx_k||²)', markersize=8)
plt.xlabel('Iteration number')
plt.ylabel('Residual norm (log scale)')
plt.title('Convergence of the CG method for a pathological example')
plt.legend()
plt.grid(True, which='both', linestyle='--', alpha=0.5)
plt.show()